题１：一盒跳棋有红、绿、蓝色棋子各15个，闭着眼睛往外拿，每次只能拿1个棋子，问至少拿几次才能保证拿出的棋子中有3个是同一颜色的？如果要求有5个棋子同一颜色，至少要拿几次？

题2：仔细观察下图1的四个空跳棋棋子的走法（红线），请根据棋子的行棋轨迹指出不一样的图（单选题）

图1

题3：如下图2，两人玩跳棋游戏，从A格开始，每次只能向上或向右或向右上跳任意格数，两人交替进行，谁能到达B格谁就赢，如果你先开始，如何保证一定能赢？

图2

解析：

（1）对于题１，至少拿7次，才能保证其中有3个棋子同一颜色。我们可以这样设想：按最坏的情况，每次拿出的棋子颜色都不一样，但从第4次开始，将有2个棋子是同一颜色。到第6次，三种颜色的棋子各有2 个。当第7次取出棋子时，不管是什么颜色，先取出的6个棋子中必有2个与它同色，即出现3个棋子同一颜色的现象。

如果要求有5个棋子同一颜色，至少要拿13次；可以类推，对于n个棋子同一颜色，至少要拿（n-1)*3+1次。本题的数学思想来源于著名的“抽屉原理”，有兴趣的童鞋可以去深入研究一下。

（2）对于题2，选a图，因为除了a图外，其他三个图的行棋轨迹都能“一笔画”完成，而a图不能一笔画写完，存在重复经过的线段。所谓的一笔画问题，其数学思想来源于数学之王欧拉提出的著名的“七桥问题”，公务员行测考试、一笔画红包、小学生数学竞赛等都有所涉及，有兴趣的童鞋可以去深入研究一下。

（3）对于题3，先手方必胜，第一步跳到图3的绿圈位置，然后保证能跳到其他打勾位置(必胜点)，即可保证必胜。本题主要考验逆向思维能力，解答过程见解说视频

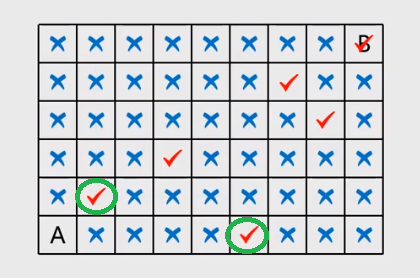
图3